Abstract
More than 60% of individuals recovering from substance use disorder relapse within one year. Some will resume drug consumption even after decades of abstinence. The cognitive and psychological mechanisms that lead to relapse are not completely understood, but stressful life experiences and external stimuli that are associated with past drug-taking are known to play a primary role. Stressors and cues elicit memories of drug-induced euphoria and the expectation of relief from current anxiety, igniting an intense craving to use again; positive experiences and supportive environments may mitigate relapse. We present a mathematical model of relapse in drug addiction that draws on known psychiatric concepts such as the "positive activation; negative activation" paradigm and the "peak-end" rule to construct a relapse rate that depends on external factors (intensity and timing of life events) and individual traits (mental responses to these events). We analyze which combinations and ordering of stressors, cues, and positive events lead to the largest relapse probability and propose interventions to minimize the likelihood of relapse. We find that the best protective factor is exposure to a mild, yet continuous, source of contentment, rather than large, episodic jolts of happiness.
1. Introduction
Illicit drug abuse remains a major problem in the United States. Despite decades of research and the implementation of policies ranging from harm reduction to punitive measures, drug overdose deaths have increased dramatically over the past 40 years, surpassing 107,000 fatalities in 2022. According to the 2021 National Survey on Drug Use and Health (NSDUH) about 3.3% of the population aged 12 and above misused opioids in 2021, the latest year for which data is available.
Our understanding of substance abuse has also evolved in the past 40 years: addiction, once viewed as a lifestyle choice, is now considered a chronic brain disease characterized by the compulsive seeking and using of drugs despite harmful consequences. Drugs change the neurocircuitry of the brain reward system leading to distortions in how non-drug rewards are processed, diminished self-control, increased sensitivity to stressful events, and the prioritization of drug consumption above all. Over time, tolerance emerges so that for pleasurable sensations to persist or for withdrawal symptoms to dampen, one must increase dosage or intake frequency. Since drug-induced damage to the brain is long-lasting and structural, treatment is a complex process, spanning several years and necessitating behavioral and pharmacological approaches. While detoxification requires a few weeks, remaining sober over a lifetime is challenging: according to the National Institute of Drug Abuse (NIDA) more than 60% of those with substance use disorder relapse within one year. The likelihood of relapse is highest in the first months after detoxification; however, relapse is possible even after many years of abstinence. Since those in recovery may have lost their previously built tolerance, de-novo consumption, even in smaller amounts than during active use, may cause overdoses.
Given the severity of the problem, it is important to understand the psychological, behavioral and environmental factors that characterize drug use. Many studies have been developed over the years to illustrate the process of addiction, utilizing psychiatric concepts, brain imaging studies, and behavioral surveys. Forecasting tools and data analyses have also been presented. There is however no explicit quantitative framework to describe the cognitive processes behind relapsing, although the presence of emotional stressors and sensory cues are known to be major influences.
Among the most vivid memories of addicts (and former addicts) is the pleasure associated with the first time drugs were consumed, often the most euphoric part of the drug-taking experience. “Chasing the first high” is a common refrain, regardless of how far in the past the first high occurred. This aligns with the so-called “peak-end” rule according to which the memory of a past experience is biased by its most emotionally intense period (the high in this case), and its ending. Other less intense periods, or even the entire duration of the experience, do not carry as much mnemonic weight. Relapses may be triggered by stressful events that lead to the retrieval of euphoric drug-related memories, such as the first high, and to the anticipation of future euphoria if drugs are consumed again. Drugs are viewed as a way to alleviate the negative affects induced by current stressors and to increase short term wellbeing. External cues such as persons, objects, locations, situations connected to past drug use may also evoke memories associated with prior drug consumption and pleasure. When stressors and/or cues are present, the associations between drug use and pleasure (or mitigation of pain) may lead to intense cravings and relapse. The goal of this work is to create a mathematical framework whereby the relapse likelihood is described as a function of quantities that represent life stressors occurring at various times and with varying intensity, cues and memories related to the previous drug addiction experience, and changes to the neurocircuitry of the former user.
In the next section, we introduce our mathematical model in which the relapse rate is framed in terms of the mental state of the user, drug availability and the presence of cues. Known psychological and behavioral processes associated with addiction, such as reward collection, tolerance, adaptation, and decision-making are integrated into a probabilistic model of relapse events. Most critical of these components is a “mental state” that is driven by positive life experiences, stressors and cues. Predictions of our model, subject to different sequences of positive events, stressors, and cues are shown in Section 3. We end with further discussion and conclusions in Section 4.
2. Dynamical systems model for relapse
2.1. Relapse rates and probabilities
We begin by assuming that drug consumption has ceased and that the individual started recovery at time . At any time of the recovery phase, the probability per unit time of relapse, defined as the instant the individual breaks sobriety by drug intake, is assumed to be driven by the user’s mental state , which can be either positive or negative, the influence of any external cues that remind the user of past drug taking euphoria, and the current availability of drugs, . Positive values of the mental state indicate well-being and optimism, and negative values represent discontent and malaise. Drug availability can be described by a continuous variable that represents the ease with which drugs are acquired and consumed. For simplicity, we binarize so that indicates that drugs are readily available and that they cannot be procured. Finally, cues are assumed to amplify the relapse rate via a non-negative motivation term . Together, we let , and shape the rate of relapse via (1)In this model, can be interpreted as the probability that the relapse event (first use of drugs after ) occurred between and . Even though the instantaneous relapse rate does not explicitly depend on history or memory, it depends on and which dynamically evolve, implicitly imparting event histories into the current relapse rate. Eq. (1) indicates that if the drug supply is unrestricted (), no cues are present (), and an individual is under a “neutral” mental state () the rate of relapse is given by a reference baseline . Negative values of the mental state increase the relapse rate, conversely vanishes in the case of a strongly positive mental state . An alternative model for may include a maximal saturated value , representing the fastest possible rate of acquiring and consuming drugs and that is attained when surpasses a positive threshold. Finally, the probability of relapsing by time , , can be written in terms of the survival (against relapse) probability up to time , given by (2)Next, we describe an event-based model for the dynamics of the mental state .
2.2. The PA/NA mental state model
The so-called “Positive Activation, Negative Activation” (PA/NA) model posits that affects arising from positive and negative experiences are not coupled and might be processed on different neural substrates. Thus a realistic representation of the mental state is as a sum of two contributions, , where positive events affect , negative ones affect , and the two evolve independently. Negative events, or stressors, are known to impact one’s mental state more than positive ones, a neurological phenomenon known as the “negativity bias”; recent studies also show that stressors tend to affect drug users more than the general population, and that drug abuse produces hypersensitivity to negative emotional distress. Note that the exponential term in Eq. (1)weights negative mental states more than positive ones, in accordance with negativity bias. We model the dynamics of and using different processing rates and as (3a)(3b)
In Eq. (3a) is the intensity of positive life event , as experienced by the individual in recovery, occurring at time and is the processing rate that returns to steady state. Similarly for , and in Eq. (3b). Since and are decoupled and , Eqs. (3a), (3b) are our mathematical representation of the PA/NA model. We solve them assuming that there are no initial affects, and that and are time-independent. Non-zero initial affects can be incorporated by setting at or at in the sequence of positive or negative life events. Time-dependent are discussed in the Appendix. We solve Eqs. (3a), (3b) under the above approximations to find (4)The mental state integrated up to time after positive and negative life events, such that and , is thus given by (5)The effects of a sequence of events defined by on the integrated mental state in Eq. (5) can be reproduced by a single event of amplitude at specific time (6)Similarly, a sequence of events generates an integrated mood that can be reproduced by single event (7)Thus far, we have modeled the dynamics of positive and negative mental state variables. Included in the relapse rate is also a dependence on random cues that trigger the memory of drug-induced euphoria. The model for cues shares many features of the negative mood variable and is described below.
Table 1. Relevant quantities and parameter ranges for the relapse models presented in Eqs. (1), (3a), (3b) (distinct mental state neurocircuitry for few positive and negative events, no cues); Eqs. (1), (19), (common mental state neurocircuitry for random, Gaussian distributed positive and negative events, no cues); Eqs. (1), (9), (36), (37) (distinct mental state neurocircuitry for uniform, positive events, subject to Poisson distributed drug-related cues) and time-dependent forms for the processing rates.
2.3. External cues
Here we discuss representations for . External cues can trigger memories of the pleasurable feelings associated with drug taking. We model these memories as impulses occurring at times whose effects decay with rate . Thus, the dynamics of , the overall motivation from cues, is given by (8)The amplitude represents the mnemonic strength of a given cue. By the peak-end rule, we assume that the most intense memory is proportional to , the largest reward response during addiction, and set for all . We also assume the decay rate associated with the permanence of the cue in one’s memory is a constant, , and that there are no initial cues, , which leads to (9)
3. Results
We now study how external stimuli and intrinsic traits affect the relapse probability . External factors include specific realizations of the and sequences, cue occurrence times and drug availability profile . The intrinsic characteristics of an individual include how his or her mental state is affected by stressors, joyous events, and cues, the processing rates for positive and negative events, and , for cues, , and the intensity of the first high . Relevant parameter ranges are listed in Table 1. Specifically, we measure time in units of days and fix /day consistent with known relapse rates of roughly 40 to 60 percent among opioid abuse disorder patients one year after treatment. We assume drugs are always available and set throughout the remainder of this work. Relapse is not possible if drugs are not available.
3.1. Dynamics without cues
We begin by studying the case of no cues and an unimpeded drug supply so that and . We first analyze the simple case of a single life event and later consider sequences of multiple negative and positive ones. Our goal is to identify which combination of events (intensity and timing) leads to the smallest relapse likelihood.
3.1.1. Longer-lasting stressors increase the relapse probability; longer-lasting positive events decrease it
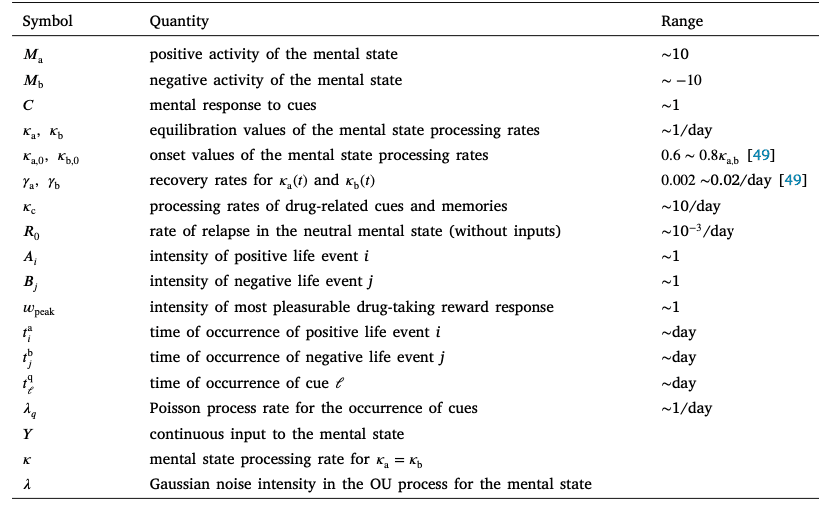
We consider a single stressor that is processed at three different rates . Fig. 1 shows that the longer the stressor affects one’s mental state (i.e. the lower ), the larger the relapse probability . Corresponding results are shown for a positive experience processed at various rates : lower values of result in smaller relapse likelihoods, as the effects of the positive event are retained for a longer time. Due to the exponential term in the relapse rate, stressors result in higher relapse likelihoods compared to positive ones of the same amplitude.
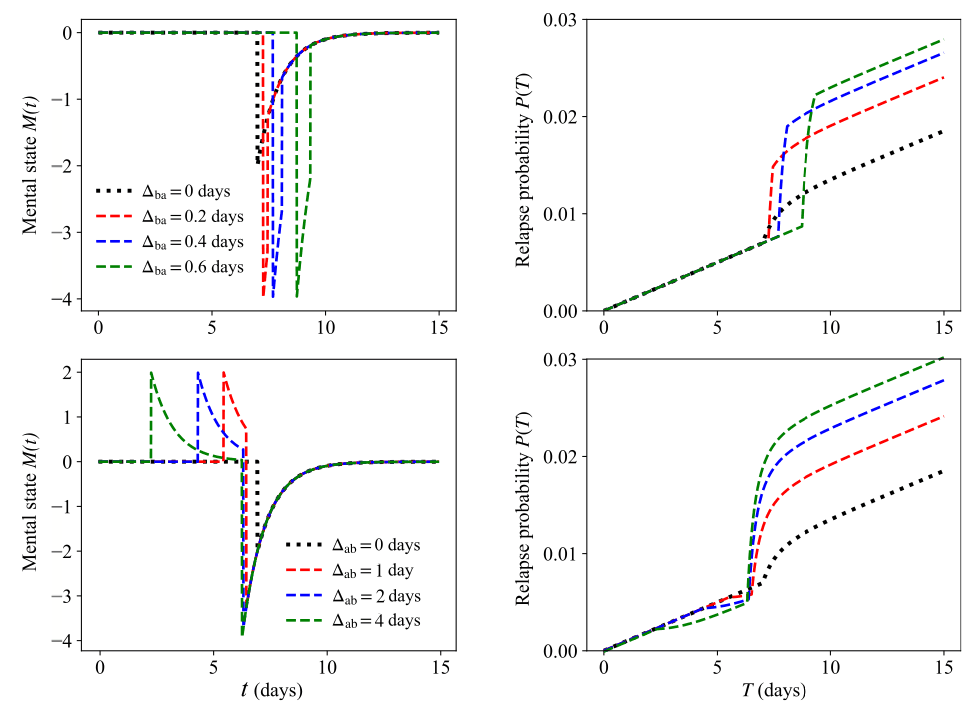
3.1.2. Clustered stressors increase the relapse probability more than disperse ones
We now include multiple life events and study how their timing affects the likelihood of relapse. Let us start with two negative events, and , that define the time interval . We then define the effective time given by (10)If (as in the “neutral” case or baseline) Eq. (10) gives ; finite values of lead to , increasing the relapse probability above that of the baseline.
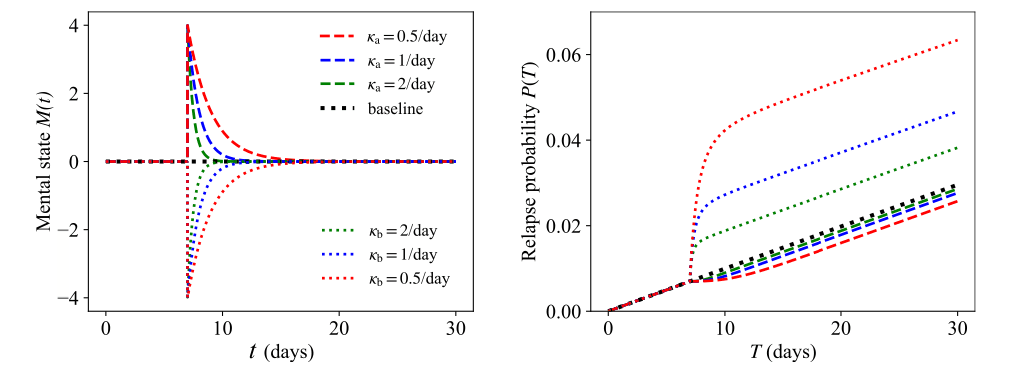
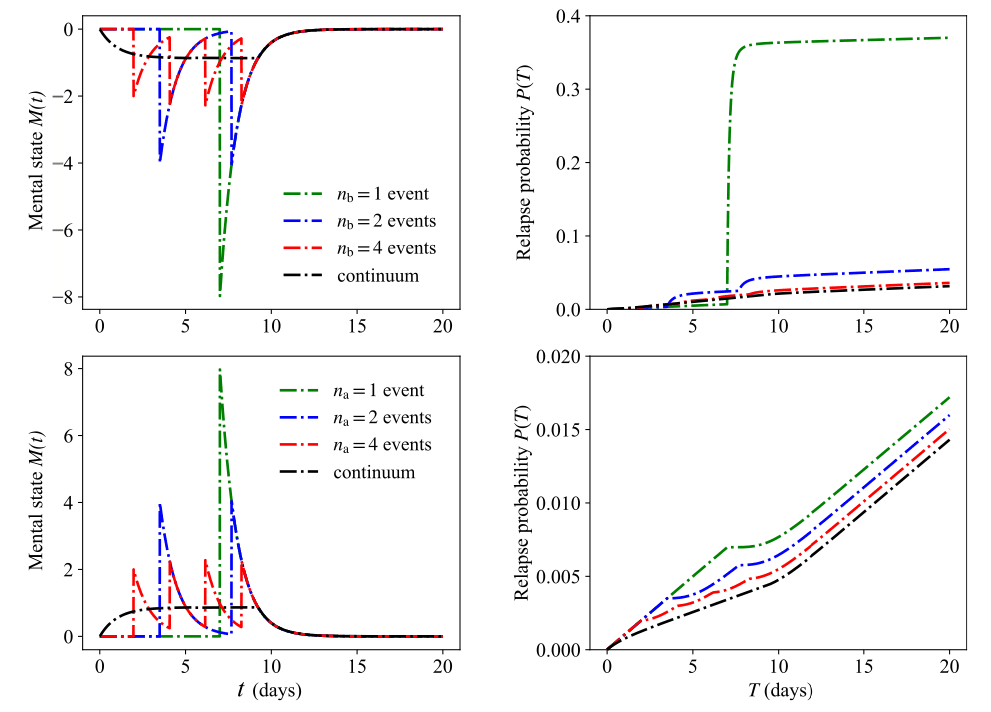
We now consider the family of paired events where the amplitudes are fixed and where are chosen such that for the two events yield the same integrated mood as the single event defined in Eq. (7). This implies that must be a constant, leaving one degree of freedom, which we choose to be . The above constraints also impose that the integrated mental state, is invariant for all paired events within the family defined by . We may now ask: within this family of paired events, where the integrated mental state is fixed, which choice of minimizes the relapse probability at any time ? We first express in terms of and , (11)and make the dependence of on explicit so that and (12)where the exponential integral . Since are fixed, the extrema of with respect to at any time are given by the zeros of (13)Regardless of , the left hand side of Eq. (13) is a negative function of , implying that has a maximum at . Since , we conclude that the largest relapse probability also occurs at ; that is, the relapse likelihood is largest when the two negative events occur simultaneously. In the top row of Fig. 2 we show the relapse probability upon exposure to pairs of stressors that belong to the same family of events with fixed and different timings . The relapse probability is indeed largest when the time lag between the two stressors is smallest, . We can apply the same arguments to more than two events and show that as the number of stressors increases, so does the likelihood of relapse. Given a negative integrated mental state generated by a set of negative events occurring within time , the relapse likelihood is largest when stressors are coincident, and is reduced when stressors are spread out. Fig. 3 shows the relapse probability for and a continuum of negative events. In our model, relapse after a single catastrophic event is more likely than after a series of smaller stressors which cumulatively yield the same integrated negative mental state as the single catastrophic stressor.
3.1.3. Dispersed positive events decrease the relapse probability more than clustered ones
We can derive similar expressions to Eq. (10) for two positive life events for which the corresponding is obtained by substituting , and , respectively. Using the same methods as for pairs of negative events, we can show that the occurrence of two positive events decreases the likelihood of relapse the most when the two events are well spaced out. Results are shown in the bottom row of Fig. 2 for pairs of positive events with fixed and different timings. The smallest likelihood of relapse occurs when the time lag between positive events is large, conversely, the likelihood of relapse is most pronounced for . In the case of multiple, positive life events, as with the findings described for negative life events, the likelihood of relapse decreases the most when an individual experiences many distributed but moderately happy events, compared to a much larger but isolated positive episode that carries the same overall impact as the distributed ones. Results for sequences of multiple events belonging to the same family are shown in the bottom row of Fig. 3 for where events are equally spaced and for a continuum of episodes. As expected, the lowest relapse probability occurs for a uniform distribution of positive events. A modest but continuous source of support is more protective against relapse than a very intense yet short-lived positive experience.
3.1.4. Relapse is least likely if a positive experience occurs immediately after a stressor
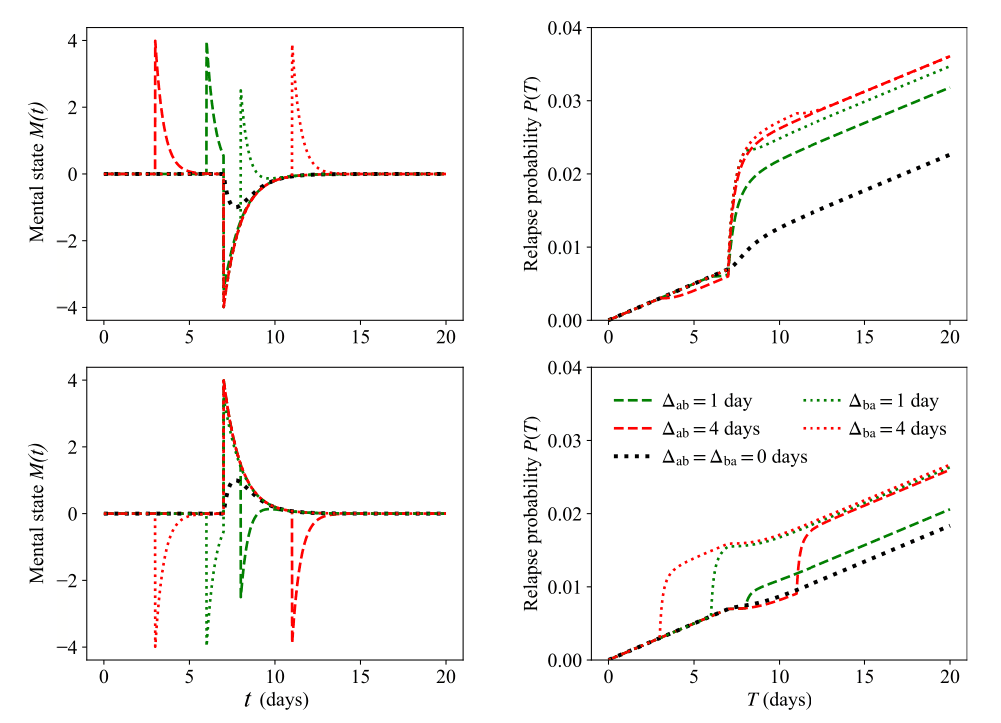
We now examine the case of a stressor followed by a positive event , where . We label the positive event rather than so that it is clear that the positive event occurs after the negative one. Given an integrated mental state and values for , the goal is to establish the lag time between the two events that minimizes the likelihood of relapse. The general case of different processing rates does not allow for easy generalization, so we set to simplify our analysis. We write in terms of and make the dependence on explicit in the expression for as follows (14)where is a constant that ensures is independent of . We can thus write (15)The left hand side of Eq. (15) is a positive function of regardless of ; as a consequence, for , is an increasing function of and attains its lowest value at . Thus, the relapse probability is also the lowest for . Once a negative life event occurs, the way to minimize the occurrence of relapses is for the individual to experience a healing, positive experience as soon as possible. Similar results hold in the case of a positive event followed by a negative event ; the relapse probability is lowest when the time lag between the two events is shortest.
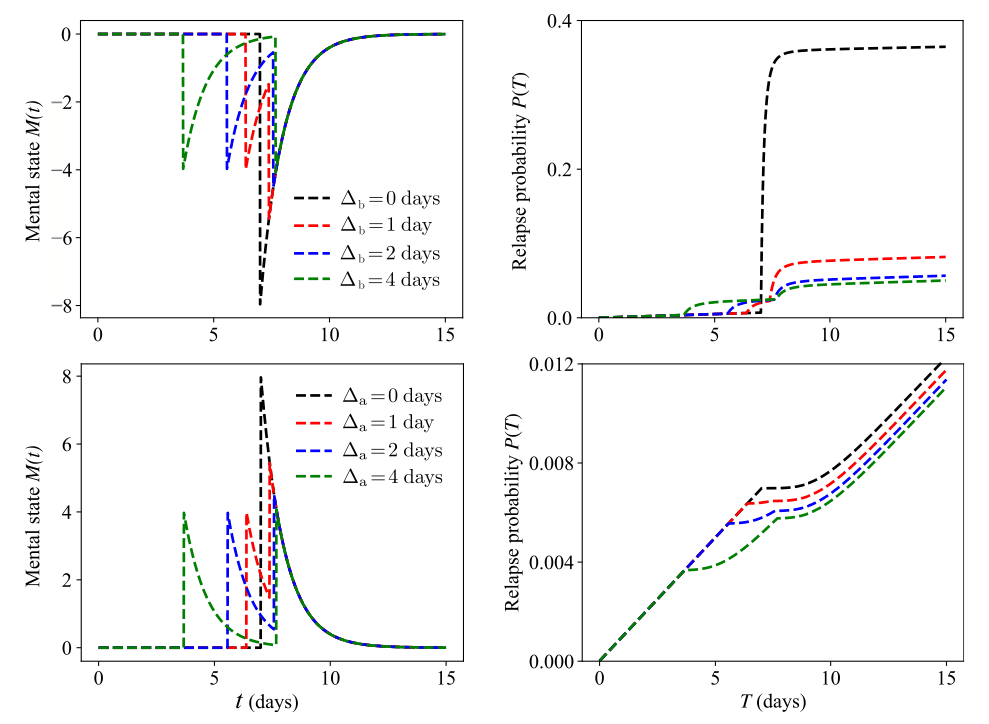
In Fig. 4 we show the relapse probability for equivalent pairs of events and that define a fixed for . For large enough , decreases with , confirming our analytic predictions. The same finding arises for equivalent pairs of events and that define a fixed for . To derive the mathematical results presented for pairs of events of amplitude , , and we assumed that no other prior events occurred; however, it is possible to show that our findings remain valid in the presence of earlier events. For example, given the events , , with processed at the same rate one can show that the relapse probability is still maximized upon clustering the two negative events and setting .
We now consider the general case . In Fig. 5 we show results for pairs of events and where and , and for pairs of events and where and . The long-term relapse probability is largely insensitive to the absolute timing of the pair of events, as long as ; however, it strongly depends on the event order and the magnitude of the time lag or . For a fixed , may depend significantly on the order of events. In general, the larger and , the less sensitive the relapse probability is to the order of events as shown by comparing the cases days with day in Fig. 5. Note that since it is impossible for the pairs of events in Fig. 5 to define the same integrated mental state for any given .
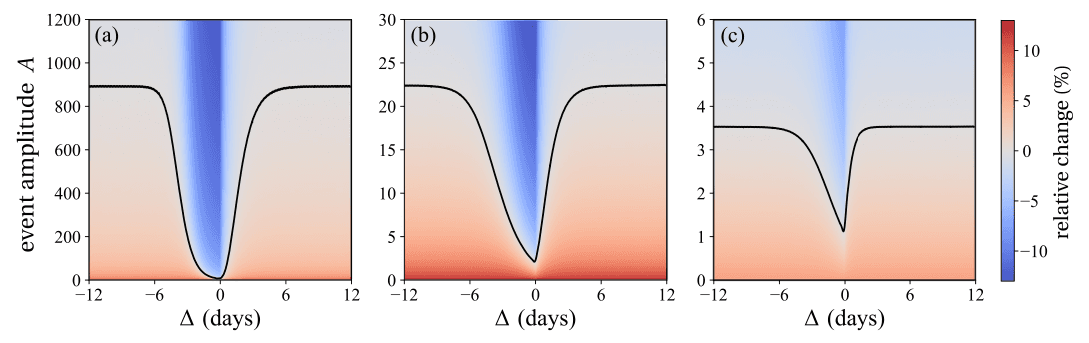
Finally, given a stressor which is processed at a rate we determine which later event processed at rate will yield the same relapse probability as the baseline case, where no events occur. To do this, we note that under the baseline, and that since it is not possible to define a single event as in Eq. (14) for , we must write in its general form (16)where . To find the value of that balances with the baseline , we must solve (17)Under the assumption , and using the identity , where is the Euler–Mascheroni constant, Eq. (17) can be simplified to (18)Eq. (18) yields the value of that neutralizes the effects of a stressor of amplitude so that at long times the relapse rate is the same as if neither event occurred. It is straightforward to show that upon substituting and Eq. (18) still holds when the order of events is reversed and the positive event occurs prior to the negative one. The black curves in Fig. 6 trace the values of that balance a stressor of amplitude given a lag time for various choices of and . These results correspond to positive values of . Vice-versa, the amplitude of a protective event that can balance a later stressor of amplitude are shown for negative values of . The asymmetry between positive and negative values of for all choices of and implies that a modest amplitude of the positive event is required to balance a fixed stressor, regardless of whether the positive event occurs before or after the stressor. The other color-coded regions in Fig. 6 show the percent increase (or decrease) of the relapse probability compared to the neutral case of no negative or positive life event, for specific values of .
3.1.5. A constant source of positivity can offset the random lows of life
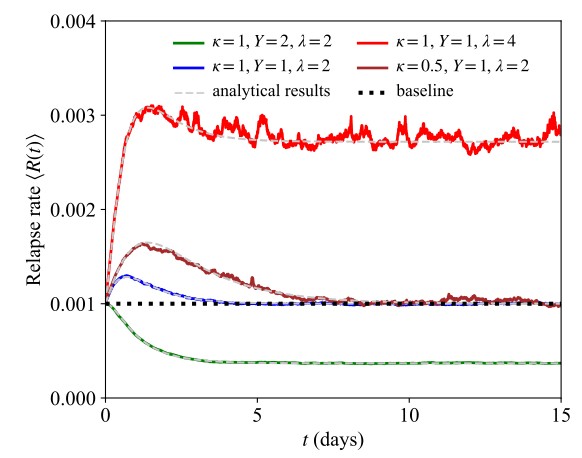
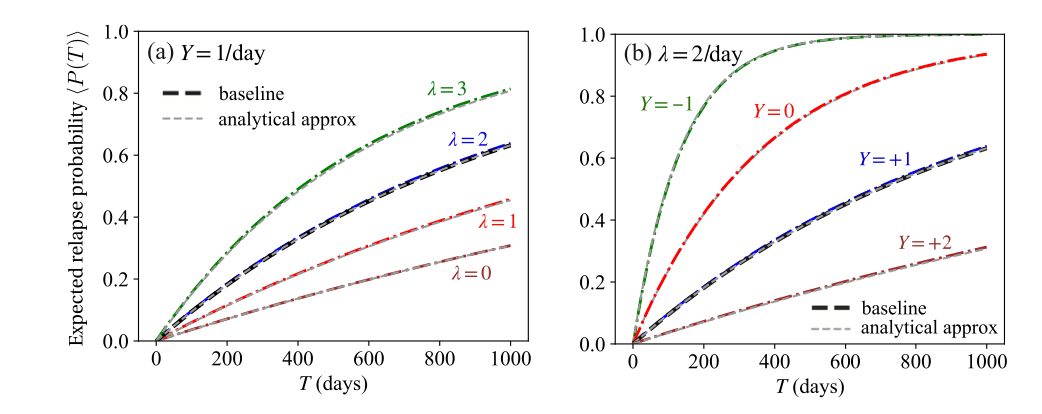
We now study the scenario in which there is a constant input to the mental state which may represent a continuous stressor or source of support. We also assume that positive and negative life events occur randomly and are processed at rates . Under these assumptions we describe the dynamics for as (19)where is a Gaussian white noise term that represents the random, positive and negative, life events. We set the general initial mental state value and write the mean and correlation function of as (20)Eq. (20) defines an Ornstein–Uhlenbeck stochastic process, a classic paradigm in statistical mechanics. The relapse rate of the neutral case, where there are no life events or continuous inputs to perturb an individual’s mental state and , is given by (21)If and , Eq. (19) can be solved as (22)Associated with Eqs. (19), (20) is a Fokker–Planck equation governing the dynamics of the probability density function (23)The solution to Eq. (23) and the initial condition is (24)In the limit , Eq. (24) defines a steady state Gaussian distribution centered at with variance . The expected time-dependent relapse rate is given by (25)which is explicitly expressed as (26a)(26b)The relapse rate in Eq. (26b) can be compared with the equivalent expression obtained in the absence of noise, i.e. for and (27)Since the above -independent ratio is always larger than one, Eq. (27) implies that unbiased noise, where positive and negative life events are equally likely in frequency and magnitude, results in a larger relapse rate than the noise-free case, regardless of the sign of . Mathematically, this result stems from the asymmetry in where the increase due to a stressor is much larger than the decrease following a positive fluctuation of similar amplitude, consistent with the brain’s negativity bias. We can also compare the general case and with the neutral case yielding (28)The values of in Eq. (28) can be tuned so that the driving term and the noise balance each other. Specifically, for the long term expected relapse rate in the presence of noise to be less than the relapse rate in the absence of any external input, the constant input must obey . Given the form for in Eq. (2), we can write the expected relapse probability as (29)and approximate it in the limit by (30)In the Appendix we discuss Eq. (29) and cases where the approximation in Eq. (30) fails, namely in the limit. Fig. 7 shows the expected relapse rate as are varied. Results derived from 100,000 simulations of the stochastic process in Eq. (19) are compared with predictions from the analytical result (Eq. (26a)). We also show the relapse rate for the baseline given by . The expected relapse rate increases with the noise amplitude and decreases with the magnitude of the positive experience and with the processing rate . Lower values imply longer processing times for all events; however, since the asymmetry in assigns more weight to negative occurrences, a larger likelihood of relapse is observed as . The corresponding values of the expected relapse probability obtained from simulations and from the analytical approximation in Eq. (30) are shown in Fig. 8.
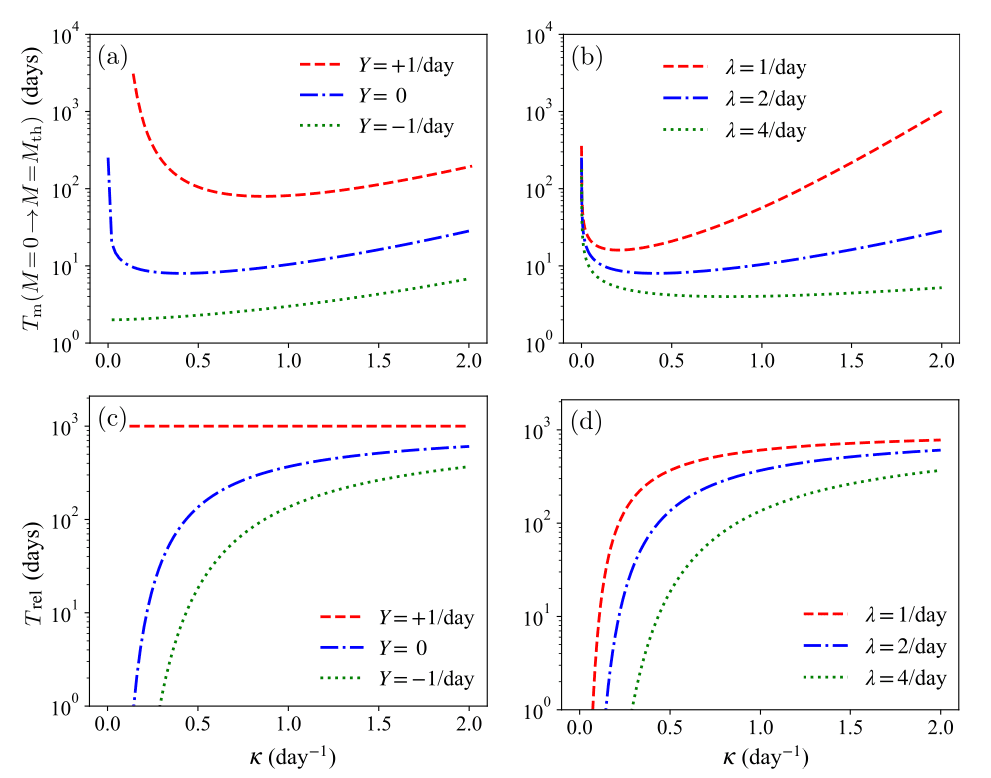
Finally, we evaluate the first passage statistics to a given mental state . Although the threshold level value can be arbitrary, we set it to be negative to represent a critically unhappy mental state. The dynamics of the mean first passage time to reach starting from a given mental state can be derived from the backward Kolmogorov equation associated with Eq. (23)(31)along with absorbing boundary conditions and . Eq. (31)can be solved using standard methods to yield (32)where is the complementary error function . Since the argument of the integrand is a positive, decreasing function of , Eq. (32) implies that is increasing in and decreasing in . This is to be expected, given that large values of tend to shift the mental state away from the lower negative threshold , and given that large values lead to larger fluctuations that are more likely to reach the negative . However, is non-monotonic with as shown in the top row of Fig. 9. Here we plot as derived from Eq. (32) and denote it as for clarity. Note that decreases with increasing at low values of and increases with at large . To understand this non-monotonicity, note that the mental state will be restored towards within a time frame after any random fluctuation. As , this implies that after each random event, very quickly and that cumulative effects of multiple past random events will be very limited. As a result, increasing when is already large will make reaching less likely and thus, the mean first passage time will increase.
On the other hand, when , will grow approximately linearly away from driven by the input while being subject to noise. Whatever the initial value of , for large enough values of and , will most likely become positive before one, or a sequence of, negative random events will lead it close to . Increasing will now lessen any positive values of , and thus accelerate reaching the threshold. Any negative values of will instead increase as is increased, and this will cause a delay in hitting . However, given the negative value of the threshold, excursions in the space will be much longer than those in the space, so that acceleration in reaching will dominate. As a result, increasing when is small will lead to a shorter mean first passage time. This effect will be more pronounced for large values of as the excursion to, and permanence in, the space will be more sustained in these cases. When are small and especially if the initial value is negative, decreases in as is increased for small values of will be much less evident, as excursions to the plane will be rare. An alternate representation of Eq. (32) is given by expanding the integrand via a Taylor series and evaluating the integral, leading to (33)where is the generalized hypergeometric function and (34)
Eqs. (32), (33) are the mean time for an initial mental state to first reach the threshold ; one may similarly determine the mean first time to relapse using Eq. (2)(35)
The last relationship arises from Eq. (30) and is valid for . We show as a function of in the bottom row of Fig. 9, using the same parameters chosen for . The mean first time to relapse is an increasing function of and a decreasing function of , indicating that positive continuous inputs and exposure to relatively small noise amplitudes can act as protective factors. These trends are consistent with those observed for .
3.2. The presence of cues
In this section, we study how cues affect the mental state and the likelihood of relapse. According to Eqs. (1), (9) sensory cues are mathematically represented as a stressor of fixed amplitude occurring at times . This description is consistent with psychiatric studies that have identified overlaps in the neural circuits that process stress and drug-related cues and that have found that both lead to cravings and heightened susceptibility to relapse. As mentioned earlier, we assume that cues always bring back memories of the first high so that the amplitude is fixed. As a result, findings illustrated in Sections 3.1.1 Longer-lasting stressors increase the relapse probability; longer-lasting positive events decrease it, 3.1.4 Relapse is least likely if a positive experience occurs immediately after a stressor still hold upon substituting for all and . In particular, relapse is less likely if a positive experience occurs immediately after being exposed to a drug-related cue and one can still utilize the results shown in Fig. 6 to determine the magnitude and timing of the positive experience necessary to balance exposure to a cue. Values of will be chosen such that , as we expect the time to process a drug-related cue to be less than the time to overcome a stressor.
Consider the case in which an individual is randomly exposed, through a Poisson processwith rate , to cues that elicit the memory of the first high. The individual thus experiences, with probability , cues within a time interval . The mean time between successive cues is . Given the equivalence between cues and stressors, these results may also be interpreted as the response to an identical stressor presented at random, Poisson-distributed times. The dynamics of the cue-induced motivation is thus (36)where are the Poisson-distributed number of events that have occurred until time . We also assume that there is a counteracting source of support to the mental state so that (37)We solve Eq. (36) with the initial condition . The resulting expression for can be used to write the relapse rate in Eq. (1) using the mental state given in Eq. (37) and under the assumption that drugs are fully available . We find (38)Using well known properties of the Poisson process shown in the Appendix we estimate the expected value of the relapse rate for any number of events occurring within time as (39)In the limit Eq. (39) can be approximated by (40)where is the Euler–Mascheroni constant. We use the approximation in Eq. (40) to evaluate the relapse rate in Eq. (2), leading to an approximate expression for , valid for (41)where (42)
In Fig. 10, we evaluate the probability of relapse at given values . We do this by first drawing a sequence of cues that occur according to a Poisson process of rate . Then, using this specific sequence of cues, we compute the relapse rate given in Eq. (38). Finally, we determine the survival probability and the relapse probability at a fixed time days using Eq. (2). The results in Fig. 10 are obtained under the assumption of no positive input, . For comparison we use the analytical approximation given in Eqs. (40), (41) to find the parameter curve corresponding to .
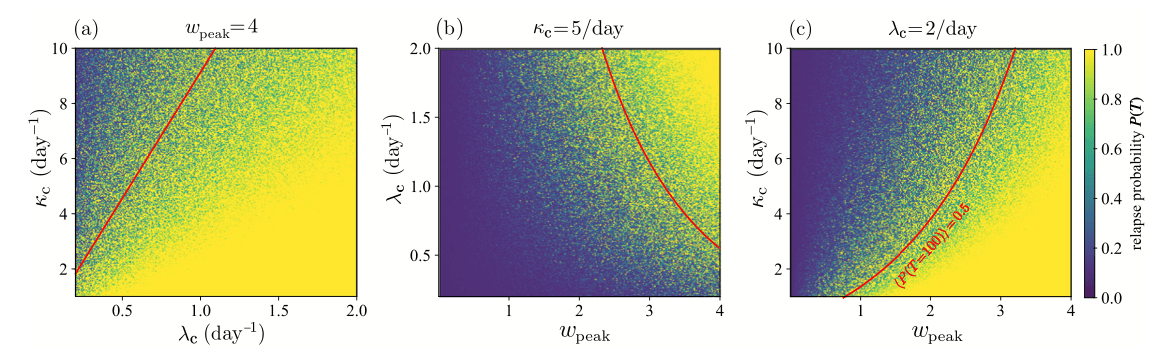
In the baseline case, where there are no cues or external stimuli, , hence the positive support will balance or alleviate the cue-induced drive to take drugs only if it satisfies (43)Thus, to be effective, the counterbalancing source of support must increase with the intensity of the memory of the first high , the rate of exposure to the cues , the duration of the cue and the processing rate of the positive events .
4. Conclusions
We presented a mathematical model for the probability of relapse in drug addiction. Our model incorporates dynamics that reflect psychiatric concepts such as the positive activation, negative activation (PA/NA) model and the peak-end rule.
Addiction research, like other studies that focus on learning, memory, rewards and synaptic plasticity, relies on neuroimaging methods to understand how the brain and its neurocircuitry adapt to short- or long-term drug use and ensuing behavioral changes. It is well documented that drug users and former users display dysregulation in their brain reward system, heightened reactivity to drug-related cues and stressors, less inhibitory self-control, and a tendency to engage in compulsive behaviors. It is also well established that the process of physical detoxification is a relatively short one, but cravings and relapse can occur even long after cessation of drug use. Relapse is often triggered by exposure to stressors or drug-related cues that the former user is unable to manage. Among the biggest limitations of neuroimaging studies and clinical trials are the need to control for individual predispositions and external circumstances, high costs, difficulties in recruiting volunteers with substance use disorder especially in longitudinal studies.
Given the complexities of addiction and the practical limitations in obtaining comprehensive data, simple and analytically tractable mathematical models may be helpful to understand how the brain responds to drugs and their absence. Decision-making and many psychiatric disorders, including addiction, have been described using quantitative mathematical models in recent years. In our work, we considered the response of the brain to a series of inputs representing positive and negative events, and how their amplitude, timing and ordering affect the likelihood that a person in recovery will use again. By construction, and mirroring the PA/NA model, negative events increase the likelihood of relapse more than positive ones of the same magnitude. We find that clustering positive or negative events is generally detrimental. For a fixed, mental state activity integrated over a fixed time frame and imparted by an arbitrary number of negative (or positive) events, the best way of distributing these events is through a continuum of moderate negativity (or positivity), rather than as a large jolt of catastrophe (or happiness) occurring at all once. On the other hand, once an individual is exposed to a stressor, a positive event occurring immediately afterward can act as a protective factor. We also found that a constant source of positive input can balance the negativity arising from a series of random events that may include large stressors. Since the mathematical representation of sensory cues in our work is akin to that of stressors, the above considerations remain valid for exposure to drug-related cues.
The effect of different environments and user profiles may be studied by tuning relevant parameters. By changing and we can represent users who respond differently to life experiences and whose memories of the “first high” vary in intensity. Similarly, the amplitudes , the Gaussian noise and the Poisson parameter can represent different risk levels in the social environment of the recovering addict. Finally, although developed in the context of relapse, our model can be used to also study the driving and protective factors that lead a non-user to try drugs for the first time. In this case, as there are no sensory cues related to past use, but can represent external stimuli that induce an individual to use drugs for the first time.
How do we translate these findings into practice? How to experience continuous positivity? Certainly, it is important to seek out positive, fulfilling experiences, embodied by the events discussed in this work. However, the continuous sources of positivity we introduced, such as the green curves in Fig. 3 and the term in Eq. (19), represent inputs to the mental state. One may interpret these inputs as arising not just from actual events, but also as imparted from a positive attitude towards life, for example through support from family and friends, finding satisfaction in one’s work, hobbies and social life. A positive attitude can also be developed through cognitive behavioral therapy, individual or group counseling or psychotherapy which are known to be effective in helping manage life’s challenges without recourse to drugs.